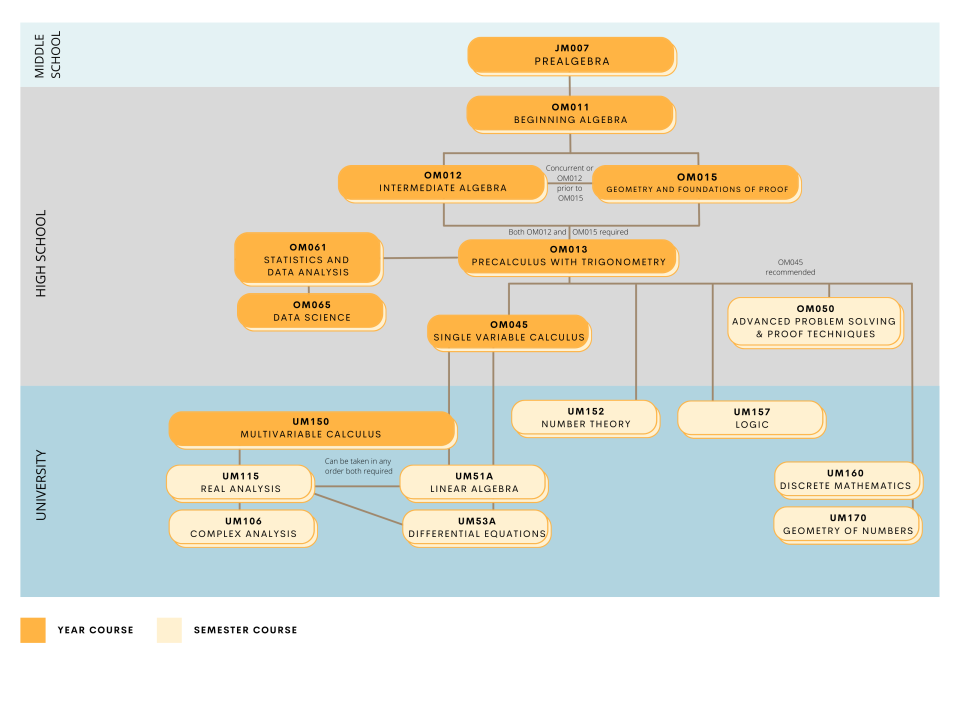
Developed in consultation with the Stanford Math Department, Multivariable Calculus offers an innovative year-long integrated treatment of Calculus in several variables together with linear algebra. This approach leads to a more comprehensive understanding of multivariable Calculus, including the geometry of Euclidean spaces, limits, partial derivatives, and optimization, along with modern matrix decomposition methods which have become the preferred method for solving large systems of linear equations in practice. This leads to a thorough presentation of integration and vector integral calculus, including volumes, iterated integrals, change of variables, applications to probability, Green's Theorem, Stokes' Theorem, and Gauss's Theorem. We also build knowledge of modern mathematical techniques crucial for applications to engineering, computer science, machine learning, economics, chemistry and other fields. These include the chain rule; least squares and linear regression for data fitting, including a more general study of n-space, all key tools necessary in modern data science; Markov chains for applications to probability, chemistry, population dynamics; singular value decomposition, which is a core idea behind image compression and other modern data-intensive work; and optimization, which is central to economics and engineering alike and is the culmination of both the Calculus and linear algebra.
Course Number
UM150
Level
University
Semester
Year-long
Credit per Semester
5.00
Subject
Prerequisites
Single-Variable Calculus (OM045) or Calculus C (OM42C) with a grade of A- or better, or an AP Calculus BC Exam score of 4 or 5, or consent of instructor
Additional Information
Advanced Problem Solving & Proof Techniques (OM050) recommended