Number Theory

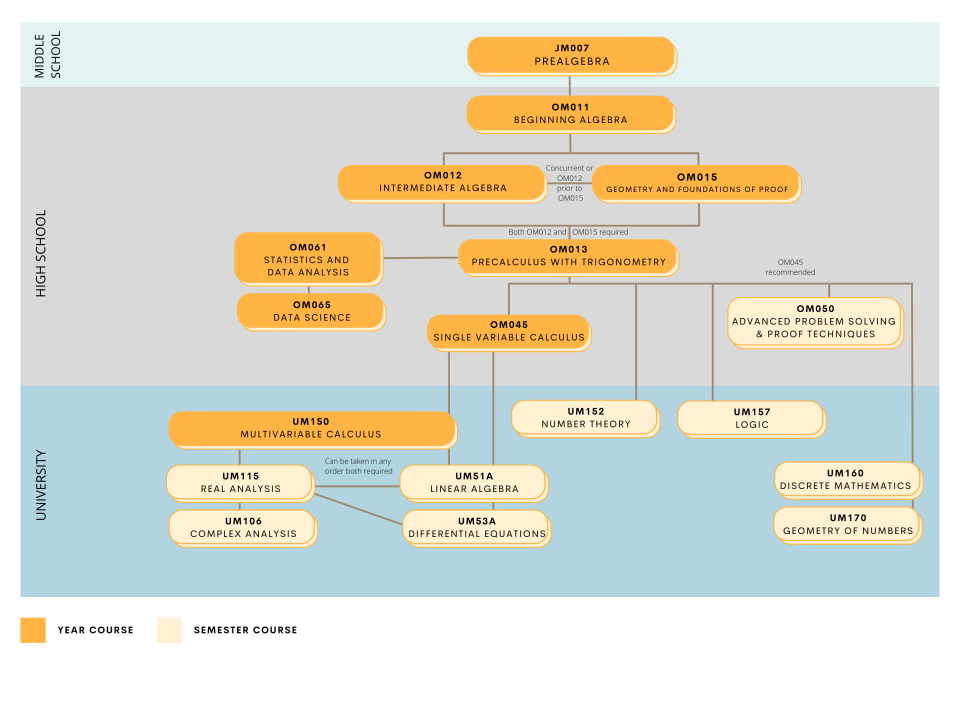
This one-semester introductory course in number theory begins with fundamental properties of the integers, including divisibility, the greatest common divisor, prime numbers, Euclid's Lemma, and the Euclidean Algorithm. Students will develop a deep understanding of modular arithmetic, the Chinese Remainder Theorem, Fermat’s Little Theorem, and the Euler-Fermat Theorem. Students will explore classical number-theoretic problems including solving Diophantine equations, quadratic residues, and primitive roots. Throughout, we will emphasize both theoretical results and practical applications, particularly in computer science and cryptography, where number theory plays a crucial role in encryption, coding theory, and algorithm design. Students will also gain experience reading and writing mathematical proofs, developing their ability to construct rigorous arguments and communicate mathematical ideas effectively.